決定木分析：クロス集計を繰り返し、予測・判別のルールを構築

分析の基準になる変数が最も偏る切り口でグループ分けをし、以降、各グループに対しても同じ操作を繰り返します。
最も偏る切り口が分類の基準への影響が大きいと判断できます。

また、各グループに含まれる変数の割合により予測ルール（モデル）を構築します。予測したい対象がどのグループに属するかがわかれば、先の予測ルールにより予測ができます。

主な適用場面として、会員になりやすい顧客の特徴を調べる、離脱しやすいページを特定する等が挙げられます。

 

また、目的変数は質的データだけでなく、量的データでも同様に分析できます。目的変数が量的データの場合は、回帰木と呼ばれます。

さらに、この決定木の概念は機械学習を習得するための基礎になります。

 

■分析例：どのような人が会員になりやすいか？

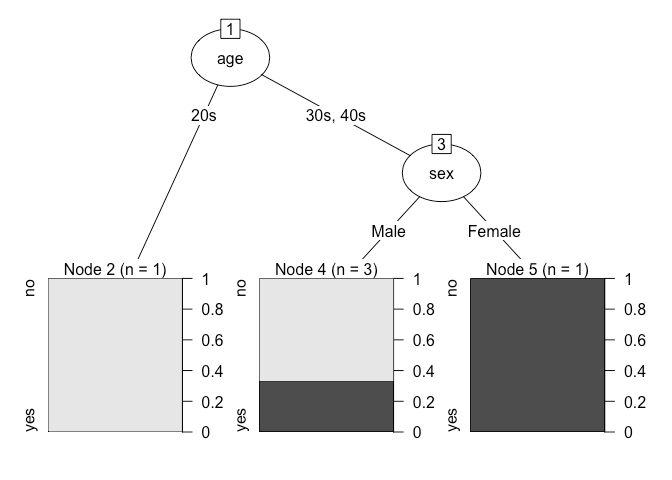
アルゴリズム

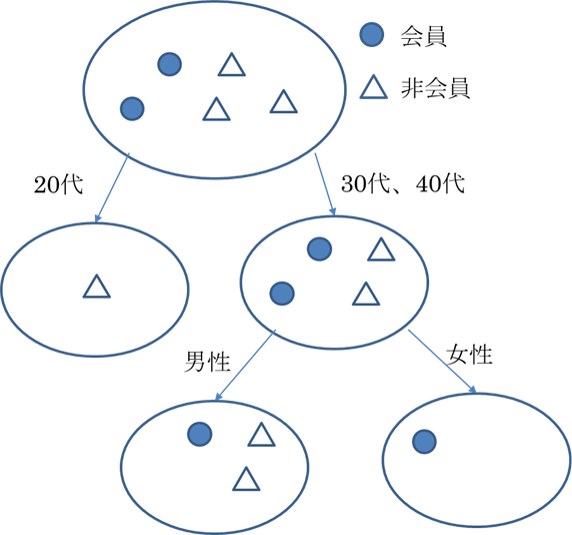
目的変数が会員、非会員の例で決定木の構築方法（アルゴリズム）を考えてみます。
分割前のデータ（図では一番上の丸の中）に対して、ある説明変数で分割して分割後の目的変数の偏りぐわい（ジニ係数）を計算します。

目的変数に影響を大きく与えている切り口（説明変数）で分割した場合は、ジニ係数は小さくなり、分割した片方で会員の割合が大きくなり、もう片方で非会員の割合が大きくなります。

これをすべての説明変数で実行し、一番ジニ係数が小さくなる説明変数（分割基準）を見つけます。分割した後のグループに対しても同じことを実行していけば、最終的にツリー構造のルールが得られます。