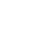- 2018年4月16日
データ分析のスペシャリストによるハンズオンセミナーです。
Rの基礎から主要な分析手法までを学べます。R初心者でも大丈夫。
詳細はこちら
- 2017年3月6日
データ分析のスペシャリストによるハンズオンセミナーです。
Rの基礎から主要な分析手法までを学べます。R初心者でも大丈夫。
詳細はこちら
- 2017年1月14日
データ分析のスペシャリストによるハンズオンセミナーです。
Rの基礎から主要な分析手法までを学べます。R初心者でも大丈夫。
詳細はこちら
- 2016年10月9日
データ分析のスペシャリストによるハンズオンセミナーです。
Rの基礎から主要な分析手法までを学べます。R初心者でも大丈夫。
詳細はこちら
- 2016年10月9日
データ分析のスペシャリストによるハンズオンセミナーです。
Rの基礎から主要な分析手法までを学べます。R初心者でも大丈夫。
詳細はこちら
- 2016年10月9日
データ分析のスペシャリストによるハンズオンセミナーです。
Rの基礎から主要な分析手法までを学べます。R初心者でも大丈夫。
詳細はこちら
- 2016年10月9日
データ分析のスペシャリストによるハンズオンセミナーです。
Rの基礎から主要な分析手法までを学べます。R初心者でも大丈夫。
詳細はこちら
- 2016年9月5日
なるべく情報を落とさずに少数の変数(次元)に要約する分析手法です。
複数項目のデータを2次元の図で視覚化する場合によく使われます。また、調査項目ごとの指向性の強さや関連性を定量化・視覚化することにも使われます。
類似する分析手法にコレスポンデンス分析があります。
属性などのカテゴリカルデータを含むデータを分析する際は、コレスポンデンス分析を使用します。
主な適用場面は、顧客の嗜好性や行動に基づくセグメンテーション、ポジショニングマップの作成が挙げられます。
■分析例:どのようなセグメントに分けることができるか?
アルゴリズム
左図のように2つの変数(x軸とy軸)で表されるデータがあります。これらを左図の斜め線(合成変数)の座標に変換し、回転すると右図になります。ここでは2変数を1変数に縮約しました。このようにして変数を合成します。
用語
・主成分(固有ベクトル):合成した変数
・主成分得点:データと主成分を掛けあわせたもの。
・固有値:主成分の情報の多少(主成分に対するデータのバラツキの大きさ)。もっとも大きい固有値に対応する主成分を第一主成分、その次に大きい固有値に対応する主成分を第2主成分と呼ぶ。
・寄与率:各主成分がデータ全体に対しどれくらいの情報を持っているかは、その主成分が対応する固有値が固有値全体に締めている割合で説明できる。この割合を寄与率、その寄与率を累積したものを累積寄与率と呼ぶ
図の解釈
一番上のグラフは主成分分析の分析結果を図示したものです。
・矢印の長さ:嗜好性の強さ(長いほどバラツキがある、違いがある)。
・矢印の向き:向きが近いほど項目間の関連性が強い。
・プロット(点):類似度の高い調査対象ほど近くにプロットされる。
- 2016年9月5日
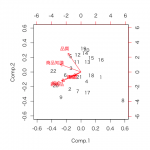
時系列データとは、対象の指標が時間に依存しているデータのことです。
例えば、株価や売上、体重など、前の観測値を基準に増減を調べるようなデータになります。
では、あなたが毎日サイコロを振って記録したとします。このサイコロの出た目の記録は時系列データでしょうか?
答えは「No」です。
前日にどんな目が出ようが、サイコロの目のそれぞれが出る確率は6分の1です(通常のサイコロでは)。つまり、前の観測値と次の観測値に関連性がないので、ここでの時系列データでないことになります。
解析時の計算や集計処理の方法が他のデータとは異なるところがあります。
時系列データを使って分析する目的は、変化のパターンを見つけることや、変化のきっかけ、変化の幅を把握することです。
大抵の場合、折れ線グラフを描画することでことたりるかと思います。
- 2016年9月5日
分析の基準になる変数が最も偏る切り口でグループ分けをし、以降、各グループに対しても同じ操作を繰り返します。
最も偏る切り口が分類の基準への影響が大きいと判断できます。
また、各グループに含まれる変数の割合により予測ルール(モデル)を構築します。予測したい対象がどのグループに属するかがわかれば、先の予測ルールにより予測ができます。
主な適用場面として、会員になりやすい顧客の特徴を調べる、離脱しやすいページを特定する等が挙げられます。
また、目的変数は質的データだけでなく、量的データでも同様に分析できます。目的変数が量的データの場合は、回帰木と呼ばれます。
さらに、この決定木の概念は機械学習を習得するための基礎になります。
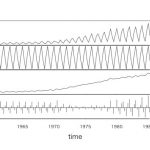
■分析例:どのような人が会員になりやすいか?
アルゴリズム
目的変数が会員、非会員の例で決定木の構築方法(アルゴリズム)を考えてみます。
分割前のデータ(図では一番上の丸の中)に対して、ある説明変数で分割して分割後の目的変数の偏りぐわい(ジニ係数)を計算します。
目的変数に影響を大きく与えている切り口(説明変数)で分割した場合は、ジニ係数は小さくなり、分割した片方で会員の割合が大きくなり、もう片方で非会員の割合が大きくなります。
これをすべての説明変数で実行し、一番ジニ係数が小さくなる説明変数(分割基準)を見つけます。分割した後のグループに対しても同じことを実行していけば、最終的にツリー構造のルールが得られます。