ランダムフォレスト

概要

ランダムフォレストとは機械学習のアルゴリズムの1つで、学習用のデータをランダムにサンプリングして多数の決定木を作成し、作成した決定木をもとに多数決で結果を決める方法です。精度、汎用性が高く扱いやすい分析手法です。

ランダムフォレストの特徴

精度が高い。
目的変数の割合に偏りがあっても、バランスが持たれる（精度をある程度保ったまま分析ができる）。
分類に用いる変数の重要度を推定する（レコメンドエンジンへ適用しやすい）。
グラフィカルに表現しにくいため、ブラックボックス化しやすい。

ランダムフォレスト分析の実行

ランダムフォレストを実行するためにパッケージrandomForestを使います。また、データはRに組み込みのデータセットTitanicを使います。

ここでは、どのような属性の人がタイタニックで生き残ったかといったモデルを作成します。また、本分析手法はランダムに並べたりする箇所があるため、実際にコードを動かしてみた結果とここに書かれている結果とやや異なるところがでくるかもしれません。

step.1 準備

# ライブラリの読み込み
library(randomForest)


# データの整形と確認
z <- data.frame(Titanic)

titanic.data <- data.frame(
  Class = rep(z$Class, z$Freq),
  Sex = rep(z$Sex, z$Freq),
  Age = rep(z$Age, z$Freq),
  Survived = rep(z$Survived, z$Freq)
)

head(titanic.data)

##   Class  Sex   Age Survived
## 1   3rd Male Child       No
## 2   3rd Male Child       No
## 3   3rd Male Child       No
## 4   3rd Male Child       No
## 5   3rd Male Child       No
## 6   3rd Male Child       No

step.2 チューニング

ランダムフォレストでのチューニング（モデルに対して任意に指定する値）箇所は、分岐に使う変数の数(mtry)です。適当なmtryを求めるためにtuneRF()関数を使います。OOB error（誤判別率）が一番低くなるmtryを採用します。

titanic.tune <- tuneRF(
  titanic.data[,-4],  # 説明変数
  titanic.data[,4],  # 目的変数
  doBest = T)  #分岐に使う変数の数(mtry)を求めるフラグ

## mtry = 1  OOB error = 21.63%
## Searching left ...
## Searching right ...
## mtry = 2     OOB error = 21.22%
## 0.01890756 0.05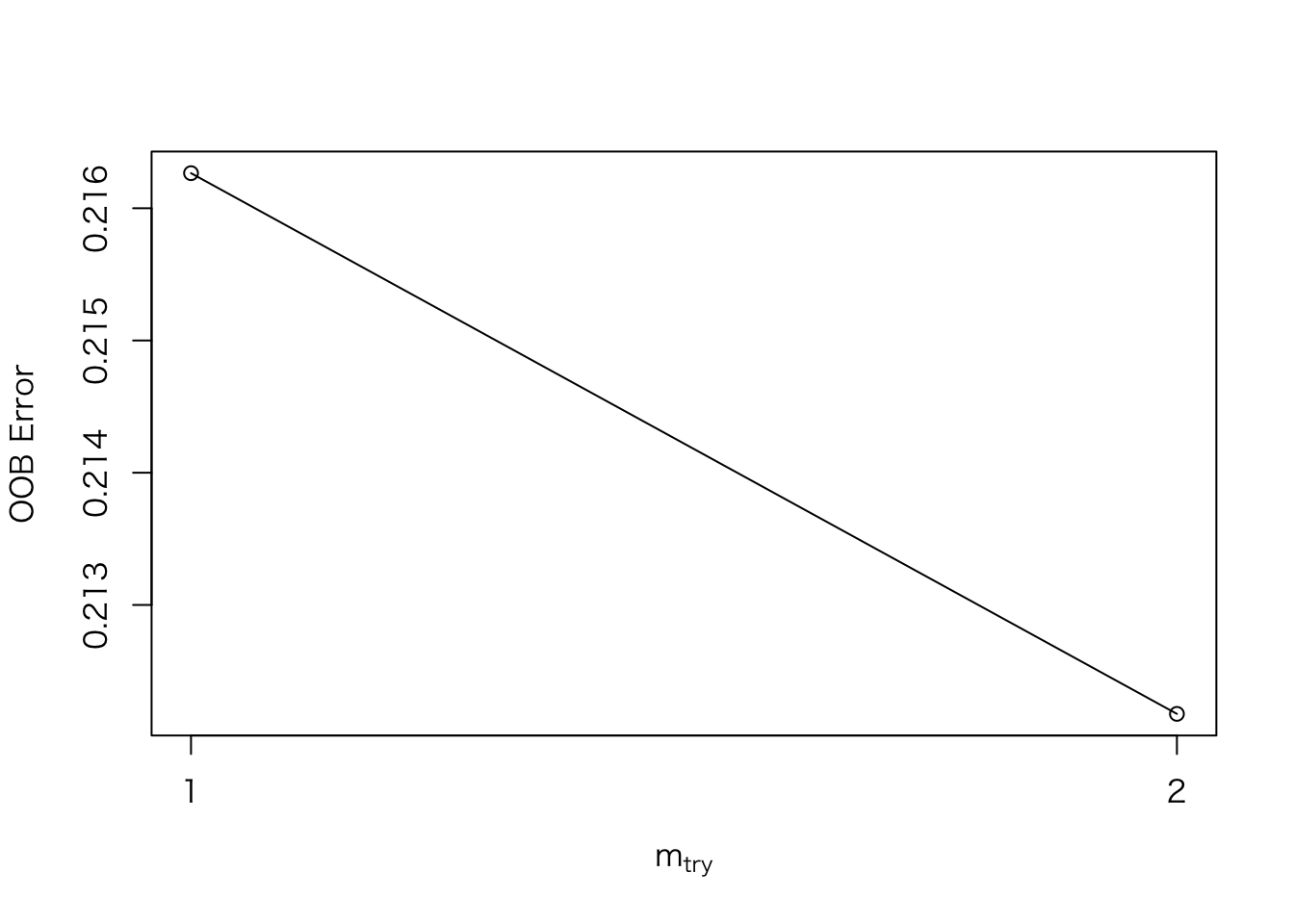

step.3 分析の実行

分析の実行にはrandomForest()関数を使用します。チューニングで求めたmtry（tuneRF()結果は、オブジェクトの$mtryに入っています）はこの関数の引数に代入します。

titanic.rf <- randomForest(  # 予測、分類器の構築
  Survived ~ .,  # モデル式
  data = titanic.data,  # データ
  mtry = titanic.tune$mtry)  # 分岐に使う変数の数

step.4 分析結果の出力

titanic.rf

##
## Call:
##  randomForest(formula = Survived ~ ., data = titanic.data, mtry = titanic.tune$mtry)
##                Type of random forest: classification
##                      Number of trees: 500
## No. of variables tried at each split: 2
##
##         OOB estimate of  error rate: 20.95%
## Confusion matrix:
##       No Yes class.error
## No  1470  20  0.01342282
## Yes  441 270  0.62025316

出力結果の読み方

OOB estimate of error rate:誤判別率
Confusion matrix:縦軸が予測数、横軸が実際の数。下の例では”No”と1911個予測したうち、実際に”No”だったものが1470個、“Yes”だったものが441個と読み取れます。

step.5 重要度順のリストを出力

それぞれの説明変数の重要度を求めるためにimportance()関数を使います。出力結果のMeanDecreaseGiniは、説明変数の影響度の大きさです。

rank <- data.frame(importance(titanic.rf))  # 重要度のリストをデータフレームに変換
rank$factor <- rownames(rank)  # 行名になっている要因をデータフレームに追加
rank <- rank[order(rank[,1], decreasing=T),]  # 重要度（偏回帰係数的なもの）順に並び替え
rownames(rank) <- 1:nrow(rank)  # ランキングを行名にする
rank

##   MeanDecreaseGini factor
## 1        186.20273    Sex
## 2         73.13773  Class
## 3         12.89348    Age

step.6 重要度順のグラフを出力

重要度の大きさをグラフに描画するためにvarImpPlot（）関数を使います。

varImpPlot(titanic.rf)