クラスター分析
概要
クラスター分析は、類似度を距離で定量化し、その類似度をもとにグループ分けをします。グループごとのデータを集計す ることで、グループの典型的な振る舞いを推定することができます。また、視覚化するために、主成分 分析やコレスポンデンス分析と併用されることが多いです。
主な適用場面は、セグメンテーション(消費者や競合、商品の分類など)が挙げられます。
クラスター分析は、階層的クラスター分析と非階層的スラスター分析に大別されます。
階層的クラスター分析
個体間の類似度に基づいて、似ている個体から順次集めてクラスターを作っていく方法で、樹形図で示すことができます。
非階層的クラスター分析
階層的クラスターに比べ計算量が少ないため、大規模データに向いています。代表的な方法としてk-means法があります。k-means法の流れは、まず任意の個数のクラスターの中心を適当に与えます。すべてのデータとクラスターの中心との距離を求め、最も近いクラスターに分類します。新たに形成されたクラスターの中心を求めます。再びデータと新たなクラスターの中心との距離から分類し、クラスターの中心を求めます。クラスターの中心の位置が変化しなくなるまで繰り返します。
階層的クラスター分析の実行
サンプルデータとしてRに組み込みのデータセットUSArrestsを使います。アメリカの都市ごとの犯罪発生率に関するデータです。
step.1 準備
# データの確認
head(head(USArrests))## Murder Assault UrbanPop Rape
## Alabama 13.2 236 58 21.2
## Alaska 10.0 263 48 44.5
## Arizona 8.1 294 80 31.0
## Arkansas 8.8 190 50 19.5
## California 9.0 276 91 40.6
## Colorado 7.9 204 78 38.7step.2 階層的クラスター分析の実行
まずデータ間の類似性(距離)を求めるために、dist()関数を使います。そして、そのデータ間の類似性をhclust()関数に入れ、階層的クラスター分析を実行します。
USA.d <- dist(USArrests)
USA.hc <- hclust(USA.d)step.3 分析結果の出力
分析結果の樹形図を描画するために、plot()関数を使います。引数のhang = -1は葉の高さを揃えます。
plot(USA.hc, hang = -1) 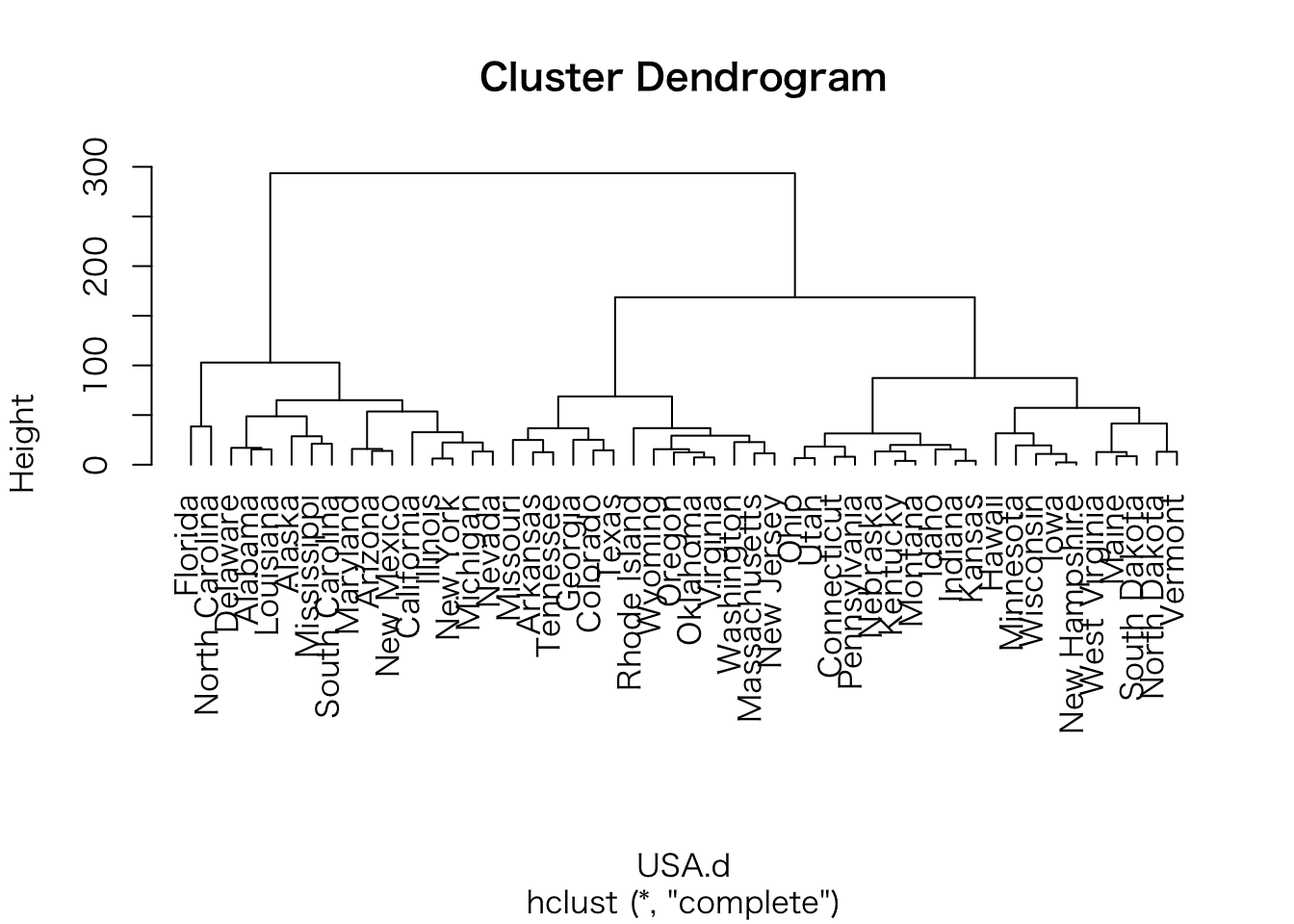
各データがどのクラスターに属するか調べるために、cutree()関数を使います。引数kはクラスターの数の設定です。次の例では4つのクラスターになることを指定しました。
cutree(USA.hc, k = 4)## Alabama Alaska Arizona Arkansas California
## 1 1 1 2 1
## Colorado Connecticut Delaware Florida Georgia
## 2 3 1 4 2
## Hawaii Idaho Illinois Indiana Iowa
## 3 3 1 3 3
## Kansas Kentucky Louisiana Maine Maryland
## 3 3 1 3 1
## Massachusetts Michigan Minnesota Mississippi Missouri
## 2 1 3 1 2
## Montana Nebraska Nevada New Hampshire New Jersey
## 3 3 1 3 2
## New Mexico New York North Carolina North Dakota Ohio
## 1 1 4 3 3
## Oklahoma Oregon Pennsylvania Rhode Island South Carolina
## 2 2 3 2 1
## South Dakota Tennessee Texas Utah Vermont
## 3 2 2 3 3
## Virginia Washington West Virginia Wisconsin Wyoming
## 2 2 3 3 2非階層的クラスター分析の実行
サンプルデータとしてRに組み込みのデータセットUSArrestsを使います。アメリカの都市ごとの犯罪発生率に関するデータです。
非階層的スラスター分析(k-means法)を実行するために、kmeans()関数を使います。2つ目の引数nstartはクラスター中心の初期値の数です。k-means法ではクラスターの中心の初期値(位置)はランダムで与え、グループ分けをします。ランダムで初期値を決めるため分析結果が安定しなくなるため、複数回グループ分け(クラスターの初期値を決めるところから繰り返す)をして結果を安定させます。この何回グループ分けをするか指定するのがnstartになります。3つ目の引数は、クラスターの数で、この数値は分析者が任意に指定します。
step.1 準備
# データの確認
head(head(USArrests))## Murder Assault UrbanPop Rape
## Alabama 13.2 236 58 21.2
## Alaska 10.0 263 48 44.5
## Arizona 8.1 294 80 31.0
## Arkansas 8.8 190 50 19.5
## California 9.0 276 91 40.6
## Colorado 7.9 204 78 38.7step.2 階層的クラスター分析の実行
非階層的スラスター分析(k-means法)を実行するために、kmeans()関数を使います。2つ目の引数nstartはクラスター中心の初期値の数です。k-means法ではクラスターの中心の初期値(位置)はランダムで与え、グループ分けをします。ランダムで初期値を決めるため分析結果が安定しなくなるため、複数回グループ分け(クラスターの初期値を決めるところから繰り返す)をして結果を安定させます。この何回グループ分けをするか指定するのがnstartになります。3つ目の引数は、クラスターの数で、この数値は分析者が任意に指定します。
USA.km <- kmeans(USArrests, nstart = 1, 4)step.3 分析結果の出力
データを2次元平面に落としこむために主成分分析を利用します。主成分分析の結果の第一主成分と第二主成分で各データの描画する位置を与え、どのクラスターに属するかで色の塗り分けをすることで、クラスター分析の結果を2次元平面上に描画します。
library(ggplot2)
USA.pca <- princomp(USArrests) #主成分分析(2次元平面のプロット用)
USA.pca.df <- data.frame(USA.pca$scores) #2次元平面用に主成分の得点をセット
USA.pca.df$cluster <- as.factor(USA.km$cluster) #クラスターの情報を付与
ggplot(USA.pca.df,
aes(x = Comp.1, y = Comp.2, label = rownames(USArrests), col = cluster)) +
geom_text() +
theme_bw(16)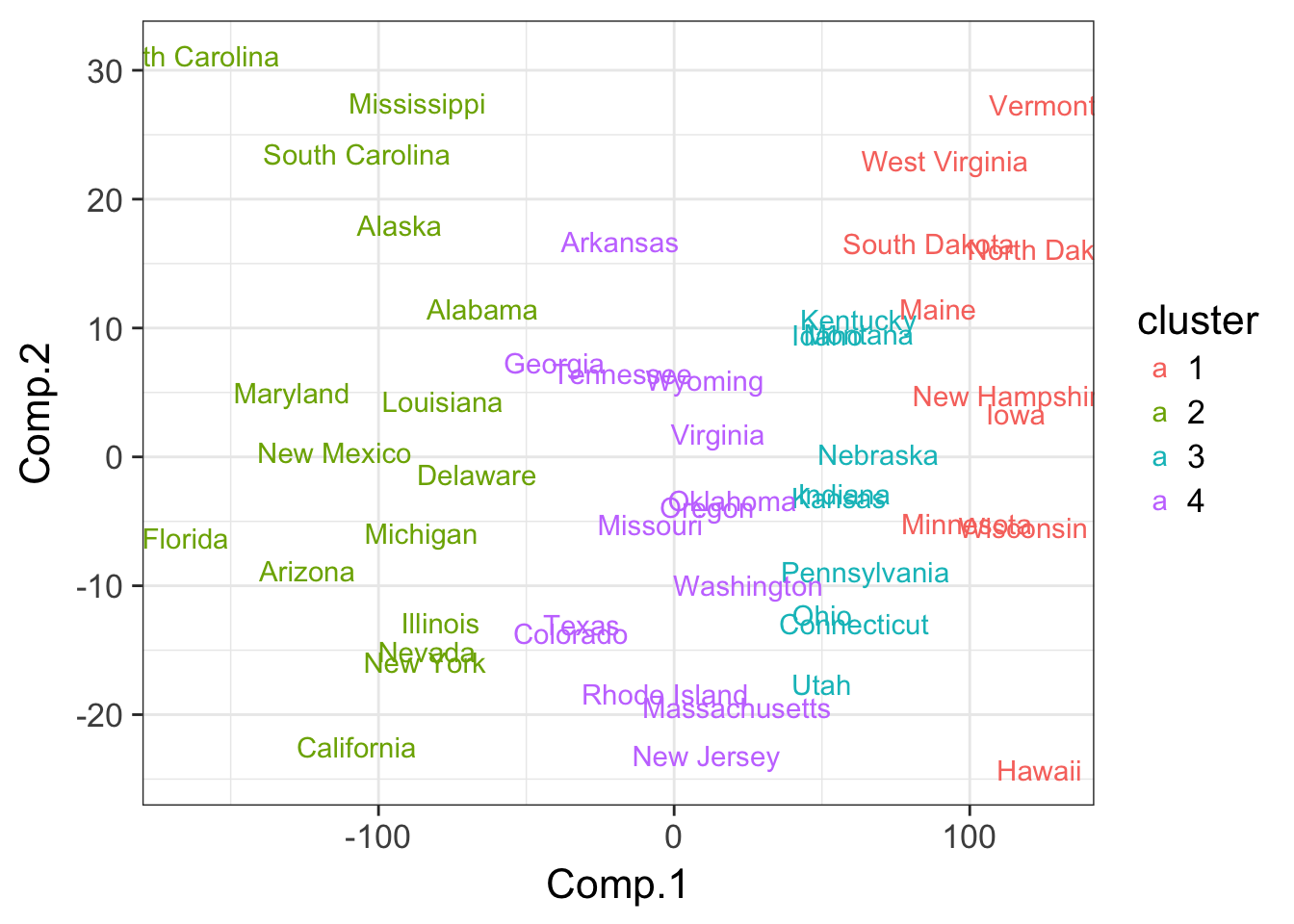
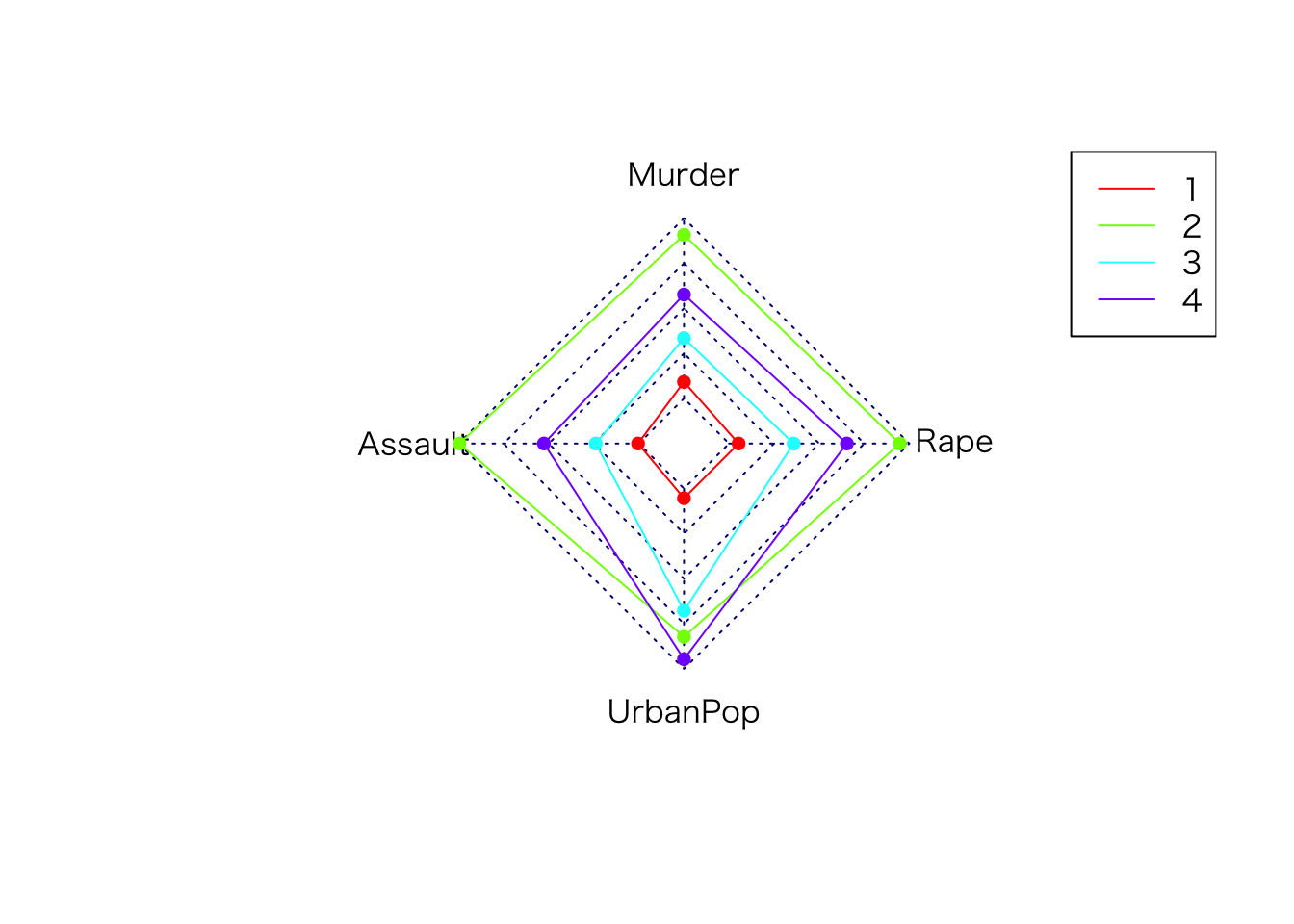
各クラスターの特徴をレーダーチャートで示します。
library(fmsb)
df <- data.frame(USA.km$centers)
dfmax <- apply(df, 2,max) +1
dfmin <- apply(df, 2,min) -1
df <- rbind(dfmax,dfmin,df)
radarchart(df, seg = 4, plty = 1, pcol = rainbow(4)) # レーダーチャートの描写
legend("topright",legend=1:4, col=rainbow(4),lty=1)