コレスポンデンス分析

概要

コレスポンデンス分析(通称:コレポン)は、調査項目間の類似関係を調査し変数を合成して、ポジショニングを直感的に理解できるマップを提供します。主成分分析と同様の分析手法ですが、量的データだけでなく、属性などの質的データ(カテゴリカルデータ)も分析できるため、適用範囲が広い分析手法です。

主な適用場面は、ポジショニングマップの作成や、クロス集計結果の視覚化が挙げられます。

(例) 年代ごとの会社ブランド評価をコレスポンデンス分析で分析

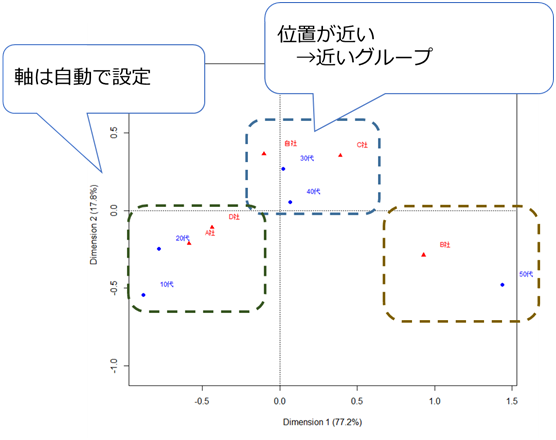
図の解釈

原点からの距離:嗜好性の強さ(長いほどバラつきがある)
原点からの方向:方向が近いほど項目間の関連性が強い
プロット(点):類似度の高い調査対象ほど近くにプロットされる

上記結果より、50 代はほぼB社を選び、10/20代はB社を選ばない、30/40代はバラつきが少ないことがわかります。

コレスポンデンス分析の実行

サンプルデータとして、パッケージMASSに組み込まれているデータセットcaithを使います。Caithはイギリスに住んでいる人の眼の色と髪の色の調査結果です。

step.1 準備

library(MASS)

# データの確認
caith

##        fair red medium dark black
## blue    326  38    241  110     3
## light   688 116    584  188     4
## medium  343  84    909  412    26
## dark     98  48    403  681    85

step.2 コレスポンデンス分析の実行

コレスポンデンス分析をするために、corresp()関数を使います。引数のnfで主成分の数を指定します。累積寄与率を計算するためにnfは行数と列数の最小値を用います。

caith.ca <- corresp(caith, nf = min(ncol(caith), nrow(caith)))

step.3 分析結果の出力

固有値の算出

関数corresp()は固有値を返さないので、正準相関を用いて算出します。固有値は、正準相関を2乗したものになります。正準相関はcorresp()の結果に、＄corとして記録されています。

caith.eig <- caith.ca$cor ^ 2
round(caith.eig,3)

## [1] 0.199 0.030 0.001 0.000

寄与率の算出

各固有値に対応する得点の寄与率は、各固有値を固有値の合計で割ることで求められます。

caith.cont  <- 100 * caith.eig / sum(caith.eig)  # 単位は％
round(caith.cont, 2)

## [1] 86.56 13.07  0.37  0.00

分析結果の描画

寄与率の高い2つの固有値に対応する得点をプロットするために、biplot()関数を使います。

biplot(caith.ca)